求star

题目#

在一个无限的 x 坐标轴上，有许多水果分布在其中某些位置。给你一个二维整数数组 fruits ，其中fruits[i] = [positioni, amounti] 表示共有 amounti 个水果放置在 positioni 上。fruits 已经按 positioni 升序排列 ，每个 positioni 互不相同 。

另给你两个整数 startPos 和 k 。最初，你位于 startPos 。从任何位置，你可以选择 向左或者向右 走。在 x 轴上每移动 一个单位 ，就记作 一步 。你总共可以走 最多 k 步。你每达到一个位置，都会摘掉全部的水果，水果也将从该位置消失（不会再生）。

返回你可以摘到水果的 最大总数 。

示例 1：

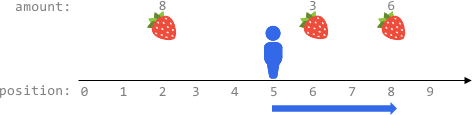
输入：fruits = [[2,8],[6,3],[8,6]], startPos = 5, k = 4 输出：9 解释： 最佳路线为：

• 向右移动到位置 6 ，摘到 3 个水果
• 向右移动到位置 8 ，摘到 6 个水果 移动 3 步，共摘到 3 + 6 = 9 个水果

示例 2：

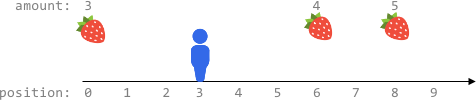
输入：fruits = [[0,3],[6,4],[8,5]], startPos = 3, k = 2 输出：0 解释： 最多可以移动 k = 2 步，无法到达任一有水果的地方

题解:key:#

①滑动窗口#

TIP

​ 假设现在已有区间[left,right],从startPos出发，至少需要多少步才能遍历该区间？

这个问题无非分为三种情况：

• startPos > right,这时需要startPos - left步
• startPos < left,这时需要right - startPos步
• left<= startPos <= right,这时有两种走法：
  • 从startPos先向左走到left然后再向右走到right，这时需要startPos - left + right -left步
  • 从startPos先向右走到right然后再向左走到left，这时需要right - startPos + right - left步
  • 总结上面两种情况，最少需要移动Math.min(|startPos - left|,|right - startPos|)步

所以可以利用滑动窗口的思想，遍历所有符合要求的最大区间，找到区间内覆盖水果的最大值

/**
 * @param {number[][]} fruits
 * @param {number} startPos
 * @param {number} k
 * @return {number}
 */
var maxTotalFruits = function (fruits, startPos, k) {
    const n = fruits.length
    let left = 0, right = 0, sum = 0, ans = 0
    //  固定窗口右边界
    while (right < n) {
        sum += fruits[right][1]
        while (left <= right && step(fruits, startPos, left, right) > k) {
            // 移动左边界
            sum -= fruits[left++][1]
        }
        right++
        ans = Math.max(ans, sum)
    }
    return ans
};
//  计算遍历区间[left,right]所需要
const step = (fruits, startPos, left, right) => {
    return Math.min(Math.abs(startPos - fruits[left][0]), Math.abs(fruits[right][0] - startPos)) + fruits[right][0] - fruits[left][0]
}